Lie E8 group and quantum criticality

Exceptional Lie E8 group shot to fame in 2007, when the US freelance physicist Garrett Lisi posted a paper on the arXiv preprint server suggesting that E8 could map out all known particles and their mutual interactions. However a well before in 1988 the Russian physicist Alexander Zamolodchikov showed that E8 symmetry could also describe the spectrum of spin excitations that occur in 1D Ising ferromagnets. Radu Coldea of Oxford University and colleagues at the Helmholtz Zentrum Berlin (HZB) have measured the energies of several of these quasiparticles by cooling the cobalt niobate to 40 mK and firing neutrons at it. When the experiment was done at zero magnetic field, five quasiparticles were spotted. Their energies are described by a mathematical formula derived three decades ago by Barry McCoy and Tai Tsun Wu.

Density of magnetic domains increases with increasing magnetic field in simmilar way, like density of gas fluctuations under pressure. At certain moment, the nested density fluctuations are formed in similar way, which we can observe during condensation of supercritical vapor. As the strength of the field was increased to the quantum critical value of 5.5 T, the ratio of energies of the first two quasiparticles approached 1.618. This number is the "golden ratio" and is precisely what should be measured if the quasiparticles are described by E8 – a prediction that was made more than 20 years ago by prof. Zamolodchikov.

As explained previously by concept of quantum foam, root system of E8 Lie group solves trivial question: "Which structure should have the tightest lattice of particles, formed by energy exchange of another particles?". And such question has perfect meaning even from classical physics point of view! Such question has a perfect meaning in theory, describing the most dense structure of inertial particles formed by energy exchange between another particles, which we can ever imagine, i.e. the interior of black hole, which is forming the vacuum. Therefore it's not so strange, both one of heterotic string theories, both Garretts E8 theory is dealing with E8 group and Horava's theory deals with quantum critical point. The animations bellow are illustrating, how most compact particle packing is related to golden mean ratio observed in critical point. By AWT the E8 is based on the geometry of most compact packing geometry possible and most dense particle packing happens when packing density along surface and volume becomes exactly balanced.

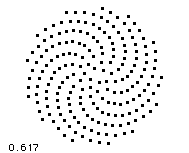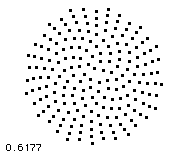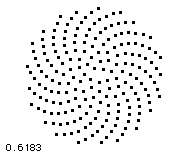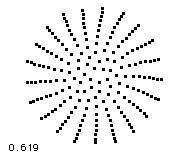
Golden mean ratio is closely related to densest particle packing in similar way, like the E8 group geometry. We can expect,  certain random arrangement of particles is more compact, then another ones, so energy spreads in slowest way and the cosmic space appears largest in it.  In natural systems golden mean minimizes the surface/volume ratio, i.e. it defines most effective object packing in situations, where many particles are involved. In such objects energy spreads in slowest possible way (because they're so compact), which means, these objects are most stable and atemporal, i.e. they're of highest fitness and they can survive easier. Human brain is just an engine for particularly slow but atemporal energy spreading (i.e. without dispersion). Solitons (not just those in human brain) consist of waves, where frequency and energy of components follows golden mean ratio, too. Evolution is analogous to travel in dispersive environment, so we can imagine particles and planets as a most compact solitons, which survived the travel through CMB noise in most successful way.

The most compact arrangement or repulsing particle corresponds so called Wigner phase inside of cold plasma crystals. Another system, which could exhibit E8 symmetry are nested density fluctuations, which occurs inside of condensing supercritical vapor temporarily. During this the nested density fluctuations of mutually repulsing particles should be formed, which leads into compact structure of kissing hyperspheres, described just by root vector system of Lie's E8 group.

We can apply the above principles to area of scientific research too. Research follows both information spreading along well defined gradients/surfaces of knowledge, i.e. formal theories, both intuitive holistic thinking through bulk of knowledge independently to existing theories (so called "crackpottery", but I rather call it a "mutations" in evolution of knowledge). After then the most effective strategy is just the approach, where the formal and intuitive approaches are balanced in golden mean ratio. So we shouldn't expect, only blind combinations of equations will lead to some TOE fast - intuitive insights and ideas are important here, too.